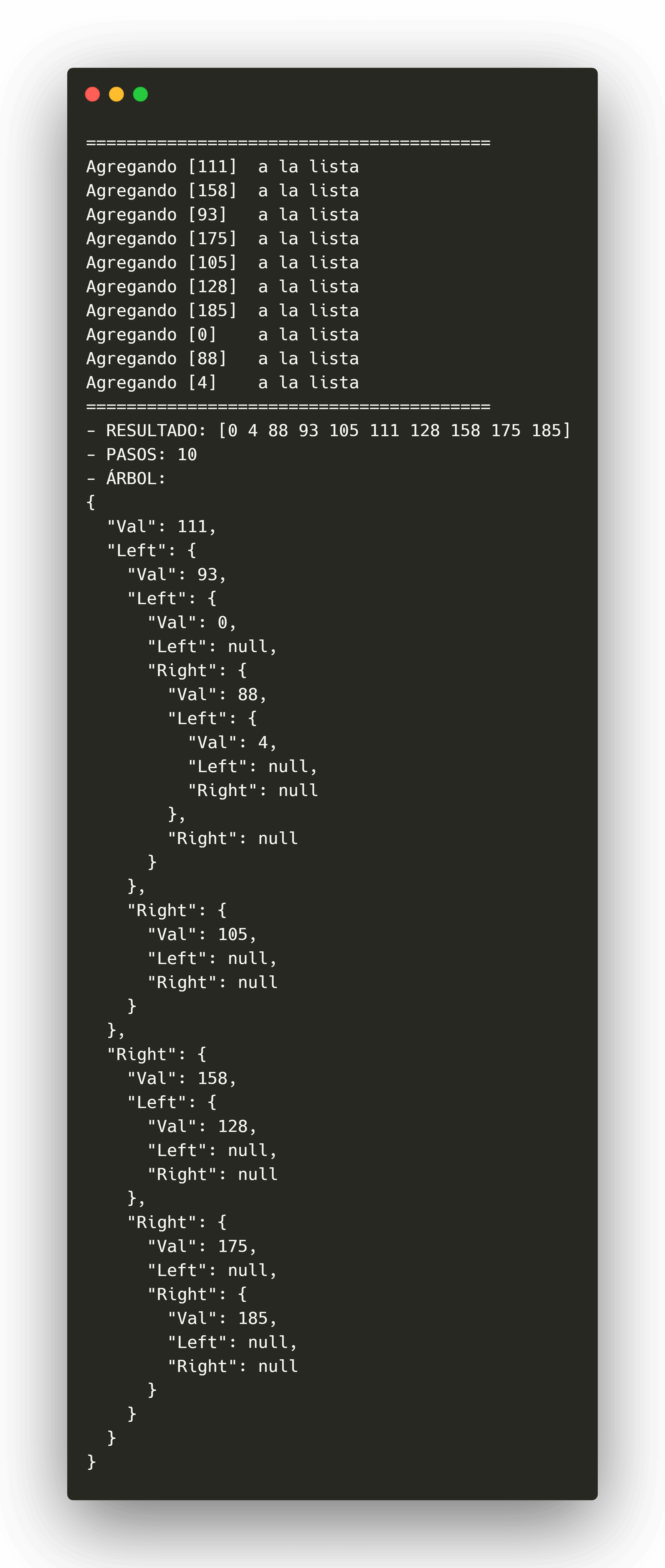
Ordenamiento con Árbol Binario | Binary Tree Sort
Repo: https://github.com/umarquez/100DaysOfC0D3/tree/master/9-binary-tree-search
Ahora que hemos avanzado un poco en la serie podemos hablar de este algoritmo que de alguna manera aprovecha el concepto de listas enlazadas para resolver el problema de ordenamiento.
Árbol binario
De igual forma que las listas enlazadas, se trata de una estructura de datos formada por nodos, pero a diferencias de las listas enlazadas simples, estos nodos pueden hacer referencia a dos nodos hijo o inferiores y ser referidos por uno superior o padre, formando una estructura de árbol con varias ramas.
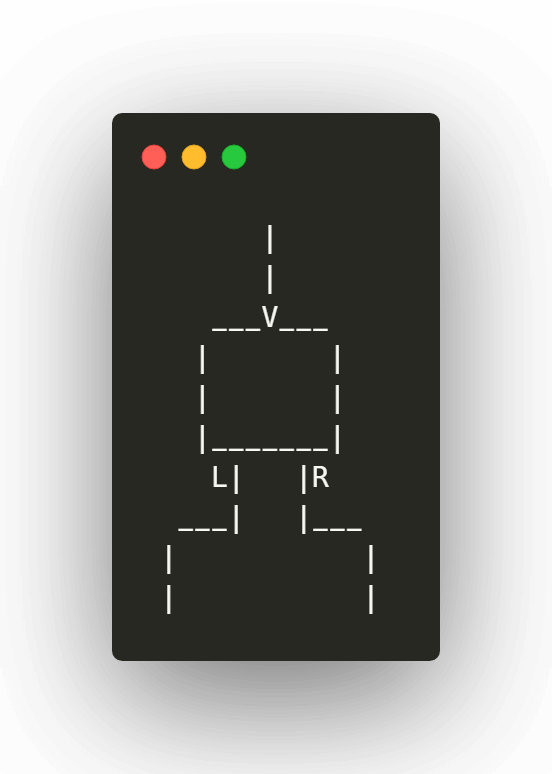
En este caso, nosotros utilizaremos una versión de este árbol, llamado: Árbol binario de búsqueda, que va almacenando los valores en las ramas del árbol de la siguiente manera:
- Compara el valor a almacenar con el primer nodo del árbol, si este es menor al valor del nodo, entonces se evalúa el nodo izquierdo, de lo contrario se evalúa el nodo derecho siguiendo la misma regla hasta no encontrar más nodos que evaluar..
- Si el nodo izquierdo o derecho estuvieran vacíos, esa será la posición final del valor, por lo que crearemos un nuevo nodo en esta ubicación y almacenaremos el valor.
Ordenamiento
Una vez que todos los valores se encuentran almacenados en sus respectivas posiciones, procedemos a recuperar los valores de cada nodo haciendo un recorrido inorden, el cuál consiste en procesar primero la rama izquierda, luego el valor actual y después la rama derecha de cada nodo.
Para tener esto más claro, vamos a realizar el siguiente ordenamiento:
Ejemplo:
Vamos a ordenar la siguiente lista de enteros:
![\[\]int{5, 7, 2, 3, 6, 1, 4}](/uploads/nYqVf0cKEiZYHJAavJLGjg.png)
Paso 1
Formamos el primer nodo con el primer valor de la lista 5:

Paso 2
Tomamos el siguiente valor 7 y lo comparamos con el primer nodo, al ser mayor lo colocamos en la rama derecha:
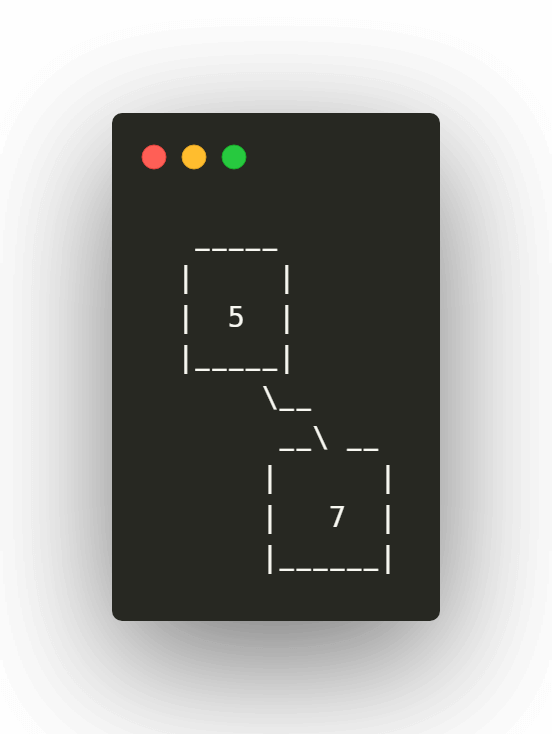
Paso 3
Ahora tomamos el siguiente elemento, lo comparamos con el primer nodo y al ser menor lo colocamos en la rama:
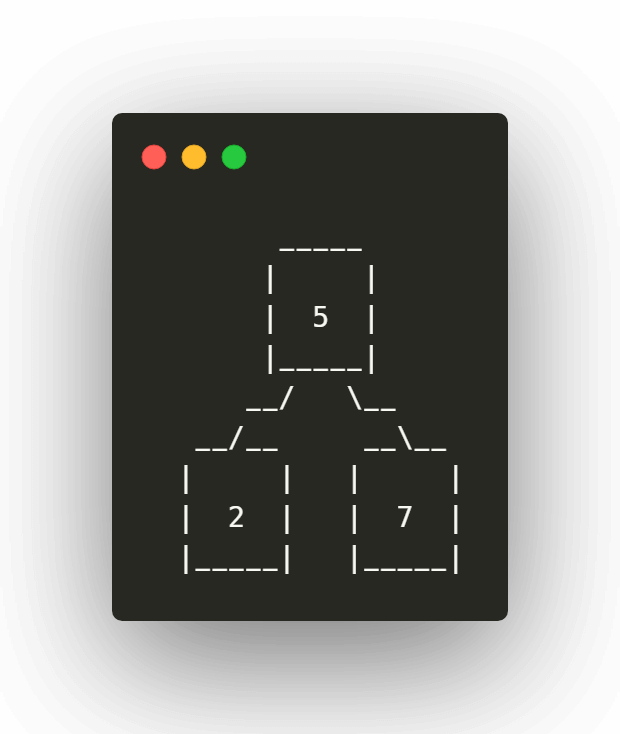
Paso 4
Tomamos el siguiente elemento 3, lo comparamos con el primer nodo, al ser menor, tomamos el nodo izquierdo y los comparamos, al ser mayor a este lo colocaremos en la rama derecha de este último nodo:
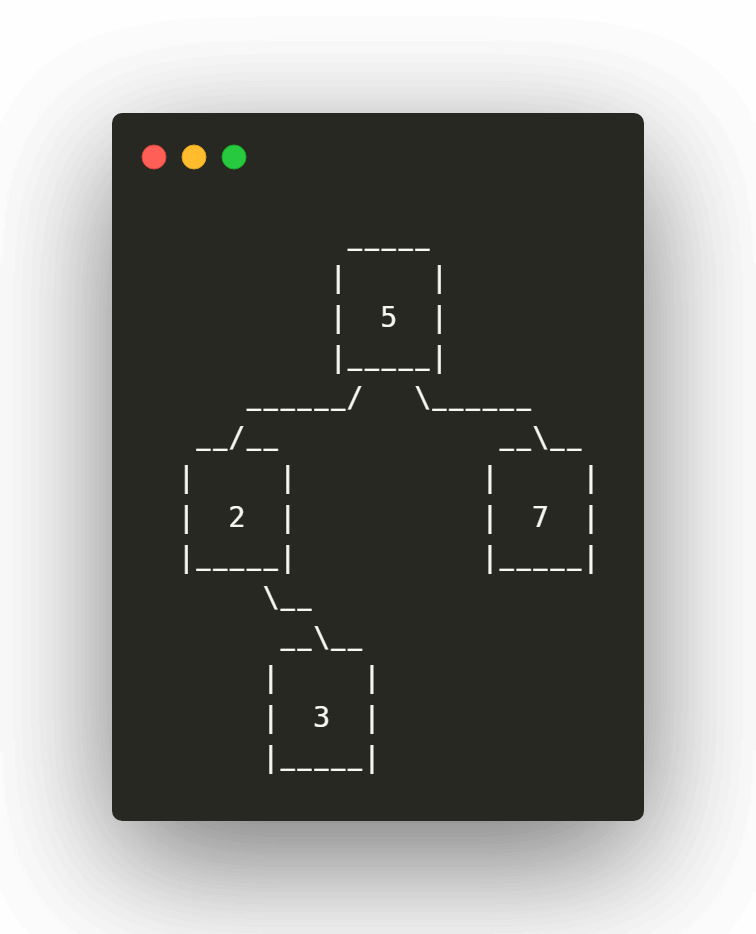
Paso 5
Tomamos el siguiente elemento 6 y lo comparamos con el primero, al ser mayor a este, tomamos la rama derecho y lo comparamos con el primer de esta, siendo menor a este, lo colocamos en la rama izquierda:
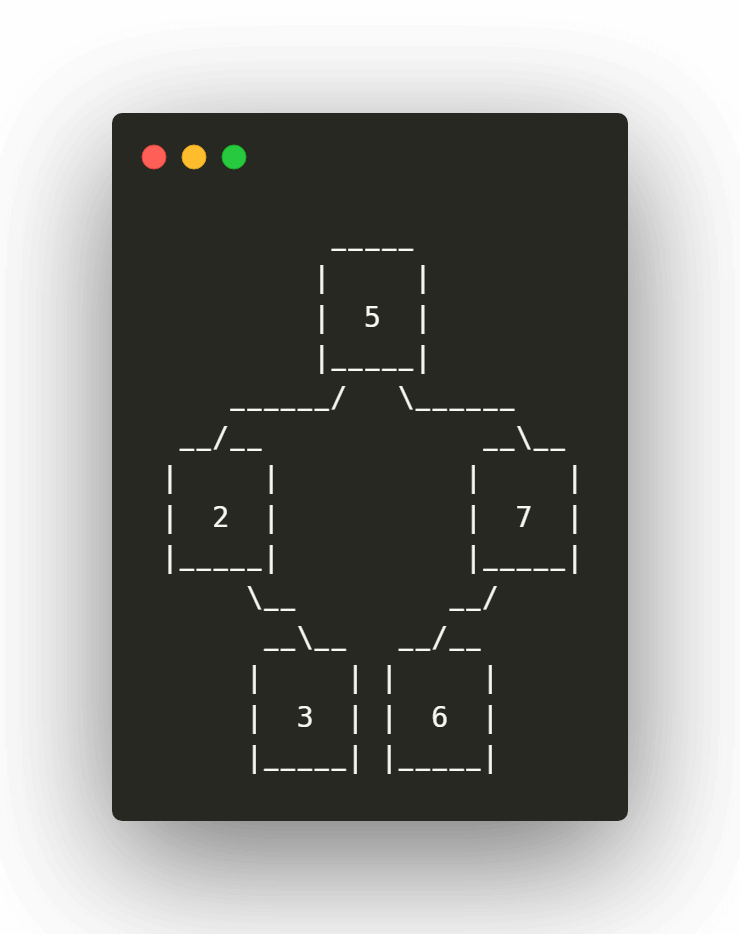
Paso 6
El siguiente elemento es el menor de la lista, así que su destino final será la rama más izquierda de todo el árbol:
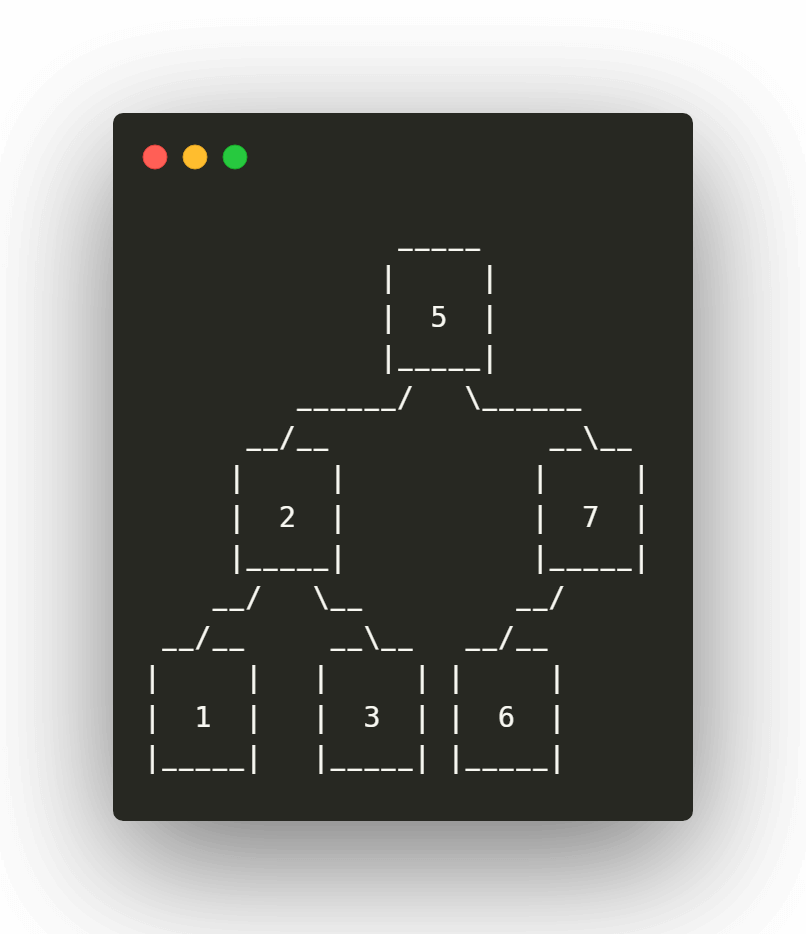
Paso 7
Por último tomamos el siguiente valor y lo comparamos con cada elemento, hasta encontrar su posición final, la secuencia completa es: 4 < 5 = L, 4 > 2 = R, 4 > 3 = R:
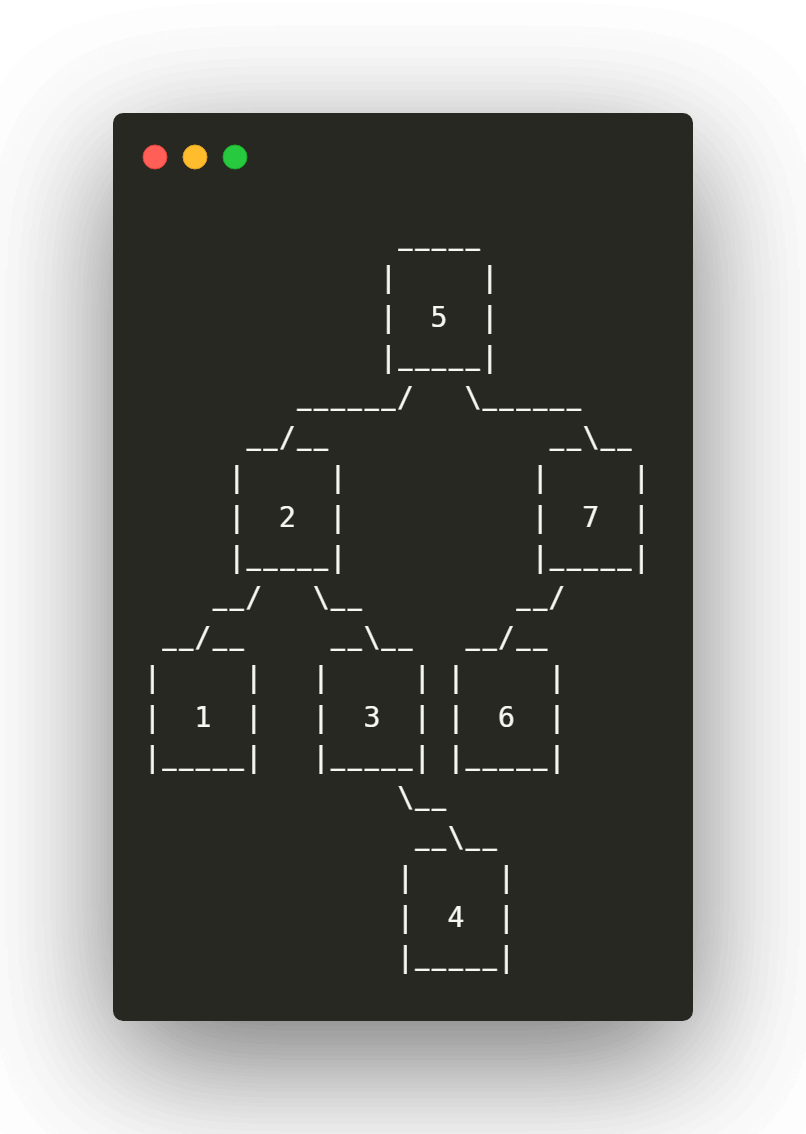
Paso 8
Ahora vamos a recorrer el árbol para recuperar los valores en orden, para ello tomamos el primer nodo y lo procesamos de la siguiente forma:
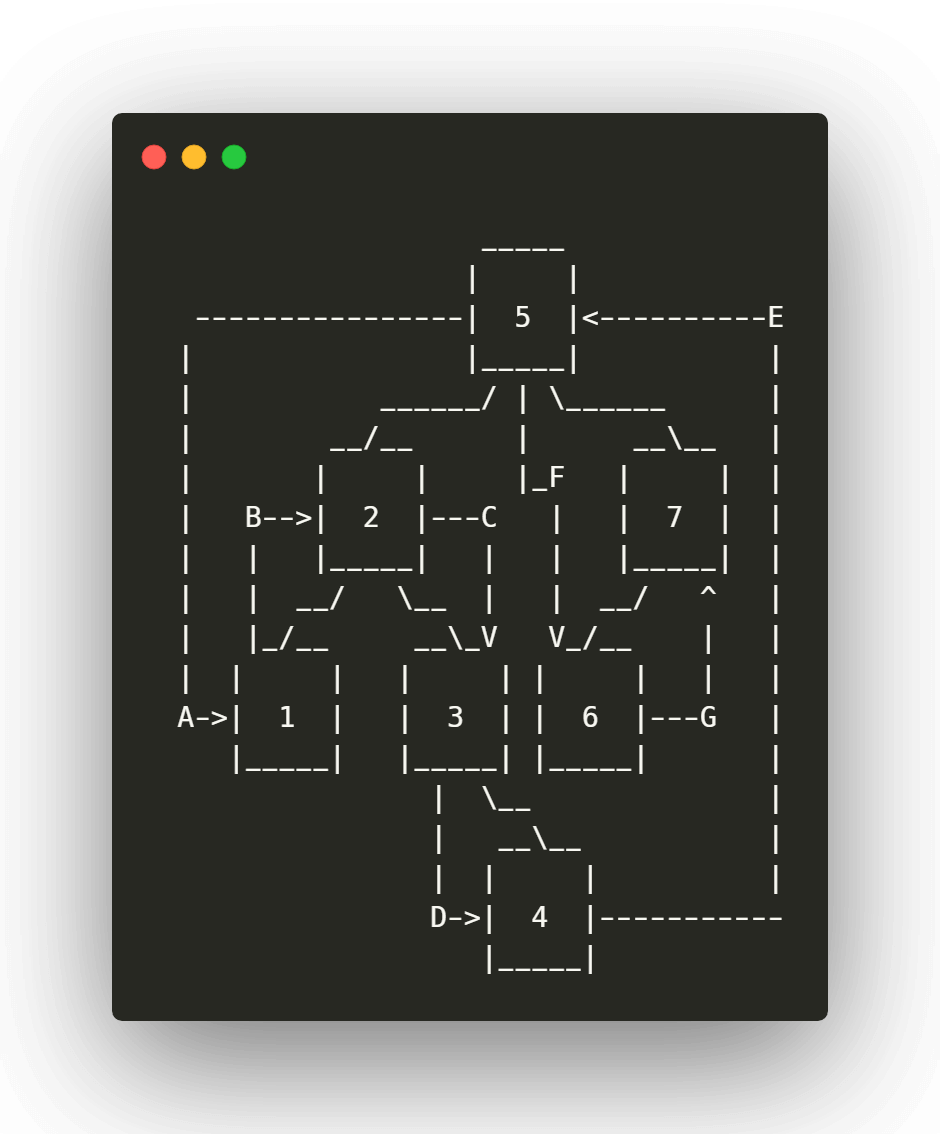
- Si este cuenta con nodo a la izquierda, lo tomamos y comenzamos el proceso de nuevo.
- Almacenamos su valor y continuamos.
- Si cuenta con nodo derecho, lo tomamos y volvemos a comenzar el proceso.
- Almacenamos su valor y continuamos.
Esto nos dará como resultado:
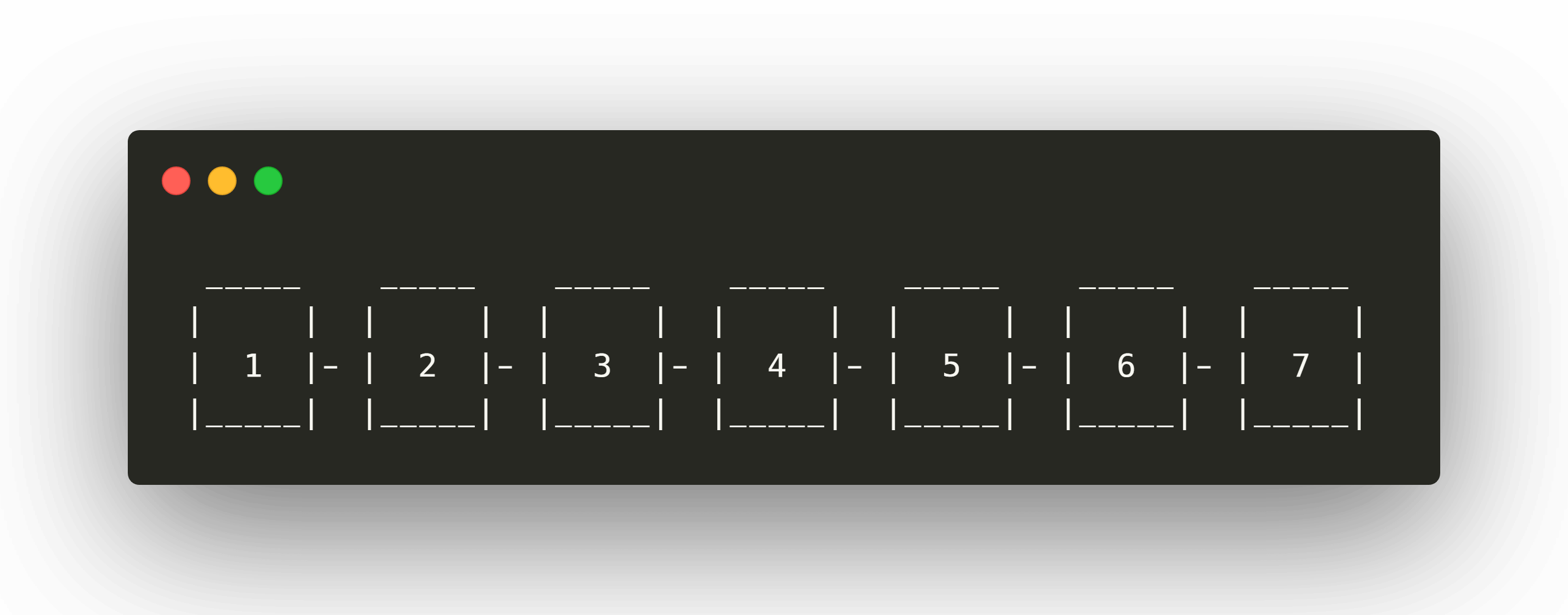
Implementación en Go
https://play.golang.org/p/1AE0i96ftt8